Zebras and tigers have stripes, cheetahs and leopards have spots, and the ocellated lizard (Timon lepidus) boasts a labyrinthine pattern of black-and-green chains of scales. Now researchers from the University of Geneva in Switzerland have demonstrated with a simple mathematical equation the lizard's complex patterns, according to a recent paper published in the journal Physical Review Letters.
“These labyrinthine patterns, which provide ocellated lizards with an optimal camouflage, have been selected in the course of evolution," said co-author Michel Milinkovitch, a theoretical physicist at the University of Geneva in Switzerland. "These patterns are generated by a complex system, that yet can be simplified as a single equation, where what matters is not the precise location of the green and black scales, but the general appearance of the final patterns."
As we've reported previously, a common popular (though hotly debated) hypothesis for the formation of these kinds of animal patterns was proposed by Alan Turing in 1952, which is why they are sometimes referred to as "Turing patterns." Turing's seminal paper focused on chemicals known as morphogens. His proposed mechanism involved the interaction between an activator chemical that expresses a unique characteristic (like a tiger's stripe) and an inhibitor chemical that periodically kicks in to shut down the activator's expression. The key is that the inhibitor diffuses at a faster rate than the activator, creating periodic patterning.

The case of the ocellated lizard is particularly tricky, since the individual scales change from one color to the other as the animal ages (green to black, black to green), producing the final labyrinthine pattern of the adults. Previously, Milinkovitch and his colleagues had modeled this gradual color-switching process using cellular automata, a computer system invented by John von Neumann and Stanislaw Ulam in the 1940s in which cells on a grid evolve in accordance with defined rules.
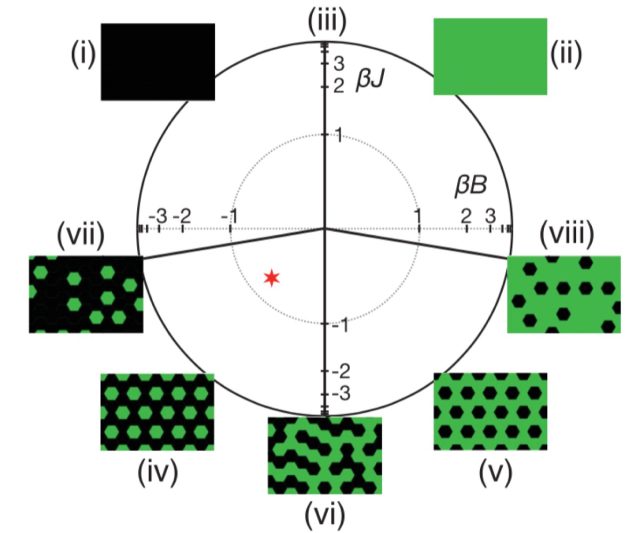
The group's computer simulations using cellular automata yielded patterns that closely resembled those seen in real-world lizards. However, the model was complicated, with 14 parameters. Milinkovitch et al. thought they could find a simpler model employing just two parameters: interactions between neighboring particles and the strength of an external magnetic field. That's the essence of the so-called Ising model.
Imagine a two-dimensional lattice, or grid. Each point on the lattice has a particle at that point with a property called "spin," and it can only be in one of two states: "spin up" or "spin down." Ideally, spins all like to be aligned with each other. They don't care if they're pointing up or down, so long as they're all pointing the same way. So over time, and under the right conditions, the spins will order themselves into that perfectly ordered arrangement. Applying a magnetic field can speed up the process by causing all the spins to flip to up or down, depending on the orientation of the field.



3175x175(CURRENT).thumb.jpg.b05acc060982b36f5891ba728e6d953c.jpg)

Recommended Comments
There are no comments to display.
Join the conversation
You can post now and register later. If you have an account, sign in now to post with your account.
Note: Your post will require moderator approval before it will be visible.