A simple mathematical model can account for lizard’s green-and-black pattern

Zebras and tigers have stripes, cheetahs and leopards have spots, and the ocellated lizard (Timon lepidus) boasts a labyrinthine pattern of black-and-green chains of scales. Now researchers from the University of Geneva in Switzerland have demonstrated with a simple mathematical equation the lizard's complex patterns, according to a recent paper published in the journal Physical Review Letters.

“These labyrinthine patterns, which provide ocellated lizards with an optimal camouflage, have been selected in the course of evolution," said co-author Michel Milinkovitch, a theoretical physicist at the University of Geneva in Switzerland. "These patterns are generated by a complex system, that yet can be simplified as a single equation, where what matters is not the precise location of the green and black scales, but the general appearance of the final patterns."

As we've reported previously, a common popular (though hotly debated) hypothesis for the formation of these kinds of animal patterns was proposed by Alan Turing in 1952, which is why they are sometimes referred to as "Turing patterns." Turing's seminal paper focused on chemicals known as morphogens. His proposed mechanism involved the interaction between an activator chemical that expresses a unique characteristic (like a tiger's stripe) and an inhibitor chemical that periodically kicks in to shut down the activator's expression. The key is that the inhibitor diffuses at a faster rate than the activator, creating periodic patterning.

The case of the ocellated lizard is particularly tricky, since the individual scales change from one color to the other as the animal ages (green to black, black to green), producing the final labyrinthine pattern of the adults. Previously, Milinkovitch and his colleagues had modeled this gradual color-switching process using cellular automata, a computer system invented by John von Neumann and Stanislaw Ulam in the 1940s in which cells on a grid evolve in accordance with defined rules.

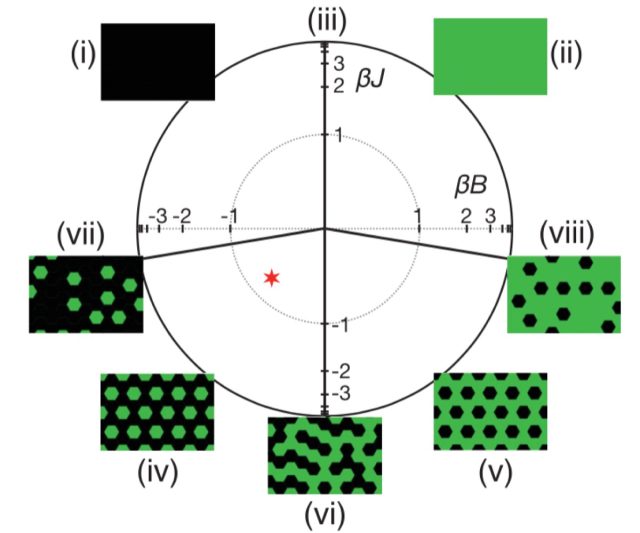
The group's computer simulations using cellular automata yielded patterns that closely resembled those seen in real-world lizards. However, the model was complicated, with 14 parameters. Milinkovitch et al. thought they could find a simpler model employing just two parameters: interactions between neighboring particles and the strength of an external magnetic field. That's the essence of the so-called Ising model.

Imagine a two-dimensional lattice, or grid. Each point on the lattice has a particle at that point with a property called "spin," and it can only be in one of two states: "spin up" or "spin down." Ideally, spins all like to be aligned with each other. They don't care if they're pointing up or down, so long as they're all pointing the same way. So over time, and under the right conditions, the spins will order themselves into that perfectly ordered arrangement. Applying a magnetic field can speed up the process by causing all the spins to flip to up or down, depending on the orientation of the field.

The Ising model starts out in that perfectly ordered state ("infinite order"), but then a new variable is introduced: temperature. We now gradually start to heat up the Ising lattice. The spins start to jiggle (because now they have more energy), and some of them start to change states (from up to down, or down to up). As the temperature gets higher, they jiggle faster and faster, until all the original order is gone because the spins are jiggling far too much. Now we have "infinite disorder"—a kind of chaos, in the physics/mathematical sense.

Now imagine that you track this gradual heating process, taking occasional snapshots at random points and noting how the arrangement of spins changes at each of those points.

Early on, you'll find almost all "spin ups" with a few clumps of "spin downs." Then there will be more and more clumping as you raise the temperature, because of this aforementioned preference for the spins to be aligned in the same direction as their nearest neighbors. You'll soon start to see more small spin-down domains of various sizes in a big sea of spin-ups. You'll know when you reach the critical point—the moment of the actual transition between phases, when the system is perfectly balanced between one phase and the other—because you will have clumps of all sizes.

“The elegance of the Lenz-Ising model is that it describes these dynamics using a single equation with only two parameters: the energy of the aligned or misaligned neighbors, and the energy of an external magnetic field that tends to push all particles toward the +1 or -1 state,” said co-author Szabolcs Zakany, a theoretical physicist at the University of Geneva in Switzerland.

So how does that apply to the ocellated lizard? The team switched from the typical square lattice of the classic Ising model to a hexagonal lattice that better reflected the structure of the lizard's skin scales. Per APS Physics:

Milinkovitch and colleagues found that the antiferromagnetic Ising model accurately recreated the time evolution of these lizards’ scale colors, the labyrinthine nature of their final patterns, and the predominant balance of green and black scales. In their model, the scales’ tendency to avoid being the same color as too many of their neighbors was analogous to the interaction between spins in an antiferromagnet, while an external forcing analogous to a magnetic field generated a slight preference for black over green scales.

Every individual lizard will have different locations of its green and black scales, but all of the patterns will have a similar labyrinthine appearance. The team hopes to extend their application of the Ising model to color patterning in other species. Another possible future study would involve linking the microscopic interactions among cells, the flipping probabilities of the mesoscopic skin scales, and the macroscopic skin color patterns.

DOI: Physical Review Letters, 2022. 10.1103/PhysRevLett.128.048102  (About DOIs).